光と色の話 第一部

第23回 光の屈折
・・・・・ 光はなぜ媒質界面で屈折するのか? ・・・・・
はじめに
本連載の第 19 回では、虹の色についてお話しました。大気中に浮遊した水滴群で太陽の光が屈折するとき、光の波長によって屈折する角度が異なることが七色の虹の発生原因でした。光学分野では光の波長に依存して屈折する角度が変わることを「分散」と呼んでいます≪※1≫。
光の屈折現象については、小中学校時代に理科の授業で勉強しました。ガラスや水の面に光が斜めに入射すると、その界面で光の進行方向が変わる現象として学習した記憶がありますね。この屈折現象の結果、右下の写真のように、水を入れた器に差し込んだ棒が、水面のところで屈曲したように見えます。
このような物理現象が起こるということ自体は小中学校で勉強するのですが、透明物質の境界で光の進行方向が何故曲がるのか?については、おそらく大学などでの専門教育で勉強することになる、というのが一般的ではないかと思います。筆者の心が屈折しているのはなかなかうまく説明できませんが、光が屈折することは論理的に比較的説明しやすいと思います。光の屈折現象については、厳密には光の波動理論によって説明されるのですが、その前に、先ず(厳密さはさておいて)直感的な理解を助けるために、デモ行進を例え話にしてお話してみましょう。

屈折現象の直感的理解・・・・・デモ行進での例え話
隊列を組んで足並みを揃えて舗装道路上を直進するデモ隊を考えます。(最近はこのようなデモ隊は流行らなくなりましたが、昔は安保闘争などでよく見かけたものです。)足並みが揃っているということは、デモ隊の構成員全員の歩幅が等しくかつ歩調(例えば、1 分間に何歩踏み出すか)が揃っているということです。
その結果、デモ隊は [歩幅] × [歩調] の行進速度で整然と直進することになります。
これを光の進行に対応付けると、歩幅が光の波長( λ [ m ] )に、歩調が振動数( ν [ 1 / 秒 ] )に対応すると考えることができ、光の進行速度( c )は
c = ν ・ λ [ m / 秒 ] となります。
このデモ隊が舗装道路から砂浜へ進入していく場合を考えます。舗装道路から砂浜へ垂直に進入する場合は、デモ隊の横一列の構成員は一斉同時に砂浜へ足を踏み入れることになります。それまでは歩き易い舗装道路上を行進してきたのですが、砂浜では歩きにくいため、歩調は一定に保っても歩幅( λ )が短くなってしまい
( λ → λ’ < λ )、その結果、砂浜に入った直後から行進速度は落ちてしまいます
( c’ = ν ・ λ’ < c )。この現象が、砂浜に足を踏み入れる横一列毎に次々に起こることになり、砂浜でのデモ隊の行進速度は、舗装道路上よりも遅くなってしまいます。しかし、横一列が一斉同時に行進速度を落とすため、デモ隊の進行「方向」自体は変わらずそのまま直進することになります。

デモ隊が砂浜へ斜め方向から進入した場合はどうなるでしょうか?右図のような場合、デモ隊の進行方向に向かって左端に位置する人が最初に砂浜に足を踏み入れることになります。この人はその時点から行進速度が落ちてしまいますが、その一方、右端の人はまだ舗装道路上ですので、それまでの速い速度のまま行進を続けています。つまり、デモ隊の横一列の構成員の行進速度が落ちるタイミングにズレが発生することになります。その結果、デモ隊の進行方向は、必然的に、舗装道路と砂浜の境界線から遠ざかる方向へ変化することになります。

デモ隊が逆の向きに(砂浜から舗装道路へ)行進する場合は、上記とは逆に、舗装道路に足を踏み入れた時点から行進速度が速くなるため、隊列の進行方向は境界線に近づく方向に変化することになります。

以上が大雑把な屈折現象の直感的イメージです。光の屈折においては、舗装道路が例えば空気に対応し、砂浜が水やガラスに対応し、「歩きにくさ」が屈折率に相当します。実際、光の速度は空気中に比べて水やガラスの中では遅くなります。つまり、屈折現象とは、媒質によって光の速度が異なることが原因となって、異なる媒質の境界面で光の進行方向が変化する現象のことであると言えます。
光の波長によって屈折角が変わる現象(光の分散)の直感的理解
光の波長が短いほど屈折率が大きくなることは、以下のように考えれば直感的に解り易いように思います。
均一媒質中での光の速度 c は、振動数 ν と波長 λ の積で表わすことができ( c = ν ・ λ )、これはデモ隊の例では、
「行進速度 = 歩調 × 歩幅」に対応することは上述しました。
砂浜では、歩調が速いほど、砂浜に足先を踏み入れる機会が多くなりますので、より歩きにくくなり、行進速度は遅くなってしまいます。これは歩調が速いほど歩幅が狭くなってしまうことに対応します。つまり、振動数 ν が大きい(波長 λ が短い)ほど、光の速度が低下してしまいます。
その結果、例えば空気(舗装道路)から水(砂浜)に進行すると、波長 λ が短いほど水面(道路と砂浜の境界)から遠ざかる方向(屈折角が小さい方向)に大きく屈折することになります。

ホイヘンス( Huygens )≪※2≫ の原理
上記の光の屈折の説明は、多少正確さは犠牲にして、例え話により直感的な解り易さを優先したものです。光の屈折や反射の現象は、理論的には波動理論に基づくホイヘンスの原理によって説明されます。
ホイヘンスの原理とは、光を振動する波として捉え、その波が伝わる媒質の各点が新たな波源として周囲の各点に振動を伝え、次々と振動が伝播していくというもので、これらの各波の波面の包絡面が実際の波として観察される、というものです。
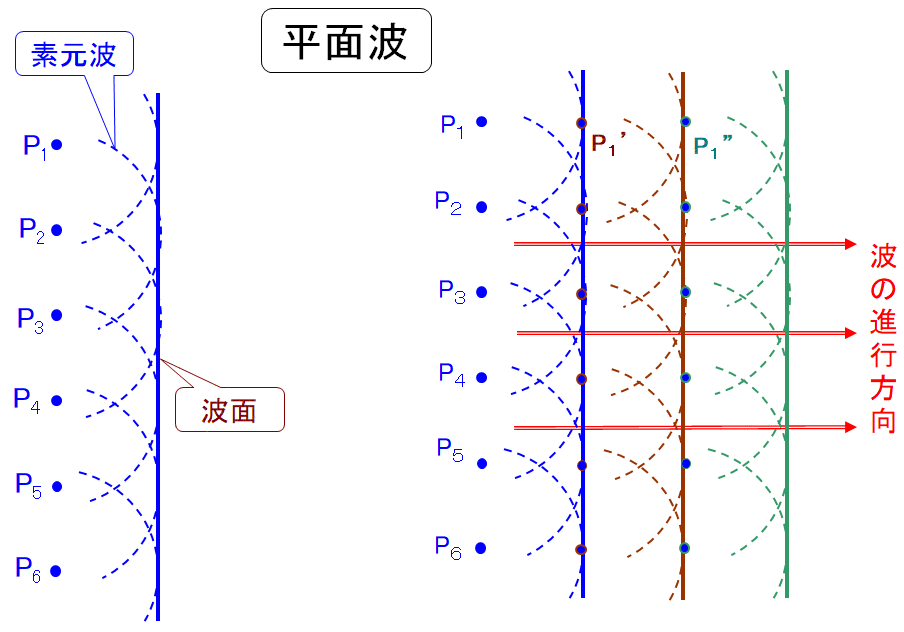
例えば平面波の場合、横一列に並んだ媒質の各点( P1 、P2 、・・・・)は同期して同一周波数で規則的に上下振動を繰り返しています。この内の1点に着目すると、この点の振動は同心円状(三次元の場合には同心球状)に周囲に波紋として広がって行くと考えられます。これを「素元波」と言います。この素元波が各点・について同時に発生すると考えられますので、結局、各素元波の共通接線す三次元の場合は共通接面すなわち包絡面)が実際の新しい波(波面)として観察されるという訳です。この波面上の各点がまた同様に新たな振動源となって、また新たな素元波を作り出し、新たな波面が生まれるということを繰り返して、波面に垂直な方向に平面波が伝播進行していくということになります。
空間の1点の振動が周囲に広がっていく場合(球面波)は、その点の周囲に発生した円形(三次元の場合には球形)の二次波(素元波)上の各点がまた新たな振動源となりそれぞれの点の周囲にまた素元波を発生させていきます。その結果、対応する素元波群の包絡線(三次元的には包絡面)も円形(球形)となり球面波が形成されます。波の進行方向は、波面に垂直な方向、すなわち、最初の震源点を中心として四方八方の全方向に均等に広がって行きます。

ホイヘンス( Huygens )の原理による屈折の説明
今、光が空気中からガラスの表面に斜めに入射する場合を考えます。この平面波を A 、B 、C 、D の 4 つの光線成分に分けて考えましょう。光は空気中では平面波として直進しています。つまり、それぞれの「素元波」 a 、b 、c 、d は同時並行的に広がって行き、それらの包絡面で構成される波面は光の進行方向に垂直な平面となります。図においては、波面を茶色(実線が「山」、破線が「谷」)で示しており、位相が揃った形で進行、入射して行く様子を模式的に描いています。
光は界面に対して斜めに入射していますので、まず光線成分 A が最初に界面 A1 に到達します。この時点で他の光線成分は、B1 、 C1 、D1 の位置まで進んでいます。界面に到達した光線成分 A はガラス(屈折率 > 1 )の内部に進行しますが、内部では進行速度が遅くなってしまいます。従って、光線成分 D が D1 から D2(界面)に到達した時点で、光線成分 A の「素元波」は a1 で示した位置まで伝播しています。同様に、光線成分 B 、C についてもそれぞれの「素元波」は b1 、c1 のような位置まで伝播しています。これらの素元波の包絡面として A2 B2 C2 D2 で示される平面が全体としての波面を構成することになり、光の進行方向はこの平面に垂直な方向となる、すなわち界面で屈折するということになる訳です。

屈折率が 1 より大きい媒質(水やガラスなど)の中では、光の進行速度は波長に依存し、波長が短い程進行速度が遅くなります≪※3≫。
従って、上記の説明において、波長が短い程、素元波 a1 、b1 、c1 の伝播速度が遅くなりますので、より大きく屈折することになります。
注釈
≪※1≫ 分散
「分散」という用語は、バラバラになることやそのバラツキの状態を表わす言葉として一般会話でもよく用いられますが、技術用語としては技術分野によって異なる定義で使用されています。
光学分野では、本文のように、光の波長(あるいは振動数)に依存して屈折角が変化することを「分散 dispersion 」と定義していますが、確率統計学分野では、確率事象のバラツキの程度を示す量である標準偏差の二乗を「分散 variance 」と言っています。(英語では、別の用語になっています。)
一般に、ひとつの用語に複数の定義があるのは、混乱の元となって好ましいことではないのですが、(光学分野と確率統計学分野のように)その用語が使用される分野が大きく離れている場合には、混乱を引き起こすことは少ないと考えられますので、事実上許容されているものと考えられます。
技術用語をどの定義の下で使用しているのかが明々白々である場合はともかく、そうでない場合は定義を明確にした上で使用すべきです。
≪※2≫ ホイヘンス Christiaan Huygens( 1629 - 1695 )
オランダの数学者、物理学者、天文学者。光学分野ではニュートンの光の粒子説に対して、ホイヘンスは光の波動説を唱え、光の反射・屈折現象を波動原理によって説明したことで有名です。
≪※3≫ 光子の進行速度( c )と波長( λ )の関係
光の発生メカニズムから説明されますように、光子のエネルギー E は、光子の振動数 ν のみによって決まります。(本連載第2回の註釈≪※2≫、≪※3≫を参照下さい。)
E = h ・ ν ( h :プランク定数 h = 6.6 × 10 -34[ J・s(ジュール・秒)])
光子が、その進行過程において、媒質(の構成分子・原子)との間でエネルギーのやり取りをするような特殊な場合を除き、一般的には媒質の種類・特性に関係なく、その光子の持つエネルギーは変化しません( E は一定)ので、異なる媒質の境界を横切ってもその前後で振動数 ν は変化しません。
光の進行速度c は、真空中で最大値 c = c0 ≒ 2.98 × 108 [ m / 秒 ](一定)となりますが、一般媒質中では
c = ν ・ λ = ( E / h )・ λ < c0
となり、真空中より遅くなり波長に比例する(波長が短いほど進行速度が遅くなる)ことになります。
デモ隊の例で言えば、舗装道路でも砂浜での歩調(振動数 ν )は一定で変わらないのですが、砂浜に進入したとたんに歩幅(波長 λ )が短くなり進行速度が遅くなることに対応します。
光と色の話 第一部

第23回 光の屈折
・・・・・ 光はなぜ媒質界面で屈折するのか? ・・・・・
はじめに
本連載の第 19 回では、虹の色についてお話しました。大気中に浮遊した水滴群で太陽の光が屈折するとき、光の波長によって屈折する角度が異なることが七色の虹の発生原因でした。光学分野では光の波長に依存して屈折する角度が変わることを「分散」と呼んでいます≪※1≫。
光の屈折現象については、小中学校時代に理科の授業で勉強しました。ガラスや水の面に光が斜めに入射すると、その界面で光の進行方向が変わる現象として学習した記憶がありますね。この屈折現象の結果、右下の写真のように、水を入れた器に差し込んだ棒が、水面のところで屈曲したように見えます。
このような物理現象が起こるということ自体は小中学校で勉強するのですが、透明物質の境界で光の進行方向が何故曲がるのか?については、おそらく大学などでの専門教育で勉強することになる、というのが一般的ではないかと思います。筆者の心が屈折しているのはなかなかうまく説明できませんが、光が屈折することは論理的に比較的説明しやすいと思います。光の屈折現象については、厳密には光の波動理論によって説明されるのですが、その前に、先ず(厳密さはさておいて)直感的な理解を助けるために、デモ行進を例え話にしてお話してみましょう。

屈折現象の直感的理解・・・・・デモ行進での例え話
隊列を組んで足並みを揃えて舗装道路上を直進するデモ隊を考えます。(最近はこのようなデモ隊は流行らなくなりましたが、昔は安保闘争などでよく見かけたものです。)足並みが揃っているということは、デモ隊の構成員全員の歩幅が等しくかつ歩調(例えば、1 分間に何歩踏み出すか)が揃っているということです。
その結果、デモ隊は [歩幅] × [歩調] の行進速度で整然と直進することになります。
これを光の進行に対応付けると、歩幅が光の波長( λ [ m ] )に、歩調が振動数( ν [ 1 / 秒 ] )に対応すると考えることができ、光の進行速度( c )は
c = ν ・ λ [ m / 秒 ] となります。
このデモ隊が舗装道路から砂浜へ進入していく場合を考えます。舗装道路から砂浜へ垂直に進入する場合は、デモ隊の横一列の構成員は一斉同時に砂浜へ足を踏み入れることになります。それまでは歩き易い舗装道路上を行進してきたのですが、砂浜では歩きにくいため、歩調は一定に保っても歩幅( λ )が短くなってしまい
( λ → λ’ < λ )、その結果、砂浜に入った直後から行進速度は落ちてしまいます
( c’ = ν ・ λ’ < c )。この現象が、砂浜に足を踏み入れる横一列毎に次々に起こることになり、砂浜でのデモ隊の行進速度は、舗装道路上よりも遅くなってしまいます。しかし、横一列が一斉同時に行進速度を落とすため、デモ隊の進行「方向」自体は変わらずそのまま直進することになります。

デモ隊が砂浜へ斜め方向から進入した場合はどうなるでしょうか?右図のような場合、デモ隊の進行方向に向かって左端に位置する人が最初に砂浜に足を踏み入れることになります。この人はその時点から行進速度が落ちてしまいますが、その一方、右端の人はまだ舗装道路上ですので、それまでの速い速度のまま行進を続けています。つまり、デモ隊の横一列の構成員の行進速度が落ちるタイミングにズレが発生することになります。その結果、デモ隊の進行方向は、必然的に、舗装道路と砂浜の境界線から遠ざかる方向へ変化することになります。

デモ隊が逆の向きに(砂浜から舗装道路へ)行進する場合は、上記とは逆に、舗装道路に足を踏み入れた時点から行進速度が速くなるため、隊列の進行方向は境界線に近づく方向に変化することになります。

以上が大雑把な屈折現象の直感的イメージです。光の屈折においては、舗装道路が例えば空気に対応し、砂浜が水やガラスに対応し、「歩きにくさ」が屈折率に相当します。実際、光の速度は空気中に比べて水やガラスの中では遅くなります。つまり、屈折現象とは、媒質によって光の速度が異なることが原因となって、異なる媒質の境界面で光の進行方向が変化する現象のことであると言えます。
光の波長によって屈折角が変わる現象(光の分散)の直感的理解
光の波長が短いほど屈折率が大きくなることは、以下のように考えれば直感的に解り易いように思います。
均一媒質中での光の速度 c は、振動数 ν と波長 λ の積で表わすことができ( c = ν ・ λ )、これはデモ隊の例では、
「行進速度 = 歩調 × 歩幅」に対応することは上述しました。
砂浜では、歩調が速いほど、砂浜に足先を踏み入れる機会が多くなりますので、より歩きにくくなり、行進速度は遅くなってしまいます。これは歩調が速いほど歩幅が狭くなってしまうことに対応します。つまり、振動数 ν が大きい(波長 λ が短い)ほど、光の速度が低下してしまいます。
その結果、例えば空気(舗装道路)から水(砂浜)に進行すると、波長 λ が短いほど水面(道路と砂浜の境界)から遠ざかる方向(屈折角が小さい方向)に大きく屈折することになります。

ホイヘンス( Huygens )≪※2≫ の原理
上記の光の屈折の説明は、多少正確さは犠牲にして、例え話により直感的な解り易さを優先したものです。光の屈折や反射の現象は、理論的には波動理論に基づくホイヘンスの原理によって説明されます。
ホイヘンスの原理とは、光を振動する波として捉え、その波が伝わる媒質の各点が新たな波源として周囲の各点に振動を伝え、次々と振動が伝播していくというもので、これらの各波の波面の包絡面が実際の波として観察される、というものです。
例えば平面波の場合、横一列に並んだ媒質の各点( P1 、P2 、・・・・)は同期して同一周波数で規則的に上下振動を繰り返しています。この内の1点に着目すると、この点の振動は同心円状(三次元の場合には同心球状)に周囲に波紋として広がって行くと考えられます。これを「素元波」と言います。この素元波が各点・について同時に発生すると考えられますので、結局、各素元波の共通接線す三次元の場合は共通接面すなわち包絡面)が実際の新しい波(波面)として観察されるという訳です。この波面上の各点がまた同様に新たな振動源となって、また新たな素元波を作り出し、新たな波面が生まれるということを繰り返して、波面に垂直な方向に平面波が伝播進行していくということになります。

空間の1点の振動が周囲に広がっていく場合(球面波)は、その点の周囲に発生した円形(三次元の場合には球形)の二次波(素元波)上の各点がまた新たな振動源となりそれぞれの点の周囲にまた素元波を発生させていきます。その結果、対応する素元波群の包絡線(三次元的には包絡面)も円形(球形)となり球面波が形成されます。波の進行方向は、波面に垂直な方向、すなわち、最初の震源点を中心として四方八方の全方向に均等に広がって行きます。

ホイヘンス( Huygens )の原理による屈折の説明
今、光が空気中からガラスの表面に斜めに入射する場合を考えます。この平面波を A 、B 、C 、D の 4 つの光線成分に分けて考えましょう。光は空気中では平面波として直進しています。つまり、それぞれの「素元波」 a 、b 、c 、d は同時並行的に広がって行き、それらの包絡面で構成される波面は光の進行方向に垂直な平面となります。図においては、波面を茶色(実線が「山」、破線が「谷」)で示しており、位相が揃った形で進行、入射して行く様子を模式的に描いています。
光は界面に対して斜めに入射していますので、まず光線成分 A が最初に界面 A1 に到達します。この時点で他の光線成分は、B1 、 C1 、D1 の位置まで進んでいます。界面に到達した光線成分 A はガラス(屈折率 > 1 )の内部に進行しますが、内部では進行速度が遅くなってしまいます。従って、光線成分 D が D1 から D2(界面)に到達した時点で、光線成分 A の「素元波」は a1 で示した位置まで伝播しています。同様に、光線成分 B 、C についてもそれぞれの「素元波」は b1 、c1 のような位置まで伝播しています。これらの素元波の包絡面として A2 B2 C2 D2 で示される平面が全体としての波面を構成することになり、光の進行方向はこの平面に垂直な方向となる、すなわち界面で屈折するということになる訳です。

屈折率が 1 より大きい媒質(水やガラスなど)の中では、光の進行速度は波長に依存し、波長が短い程進行速度が遅くなります≪※3≫。
従って、上記の説明において、波長が短い程、素元波 a1 、b1 、c1 の伝播速度が遅くなりますので、より大きく屈折することになります。
注釈
≪※1≫ 分散
「分散」という用語は、バラバラになることやそのバラツキの状態を表わす言葉として一般会話でもよく用いられますが、技術用語としては技術分野によって異なる定義で使用されています。
光学分野では、本文のように、光の波長(あるいは振動数)に依存して屈折角が変化することを「分散 dispersion 」と定義していますが、確率統計学分野では、確率事象のバラツキの程度を示す量である標準偏差の二乗を「分散 variance 」と言っています。(英語では、別の用語になっています。)
一般に、ひとつの用語に複数の定義があるのは、混乱の元となって好ましいことではないのですが、(光学分野と確率統計学分野のように)その用語が使用される分野が大きく離れている場合には、混乱を引き起こすことは少ないと考えられますので、事実上許容されているものと考えられます。
技術用語をどの定義の下で使用しているのかが明々白々である場合はともかく、そうでない場合は定義を明確にした上で使用すべきです。
≪※2≫ ホイヘンス Christiaan Huygens( 1629 - 1695 )
オランダの数学者、物理学者、天文学者。光学分野ではニュートンの光の粒子説に対して、ホイヘンスは光の波動説を唱え、光の反射・屈折現象を波動原理によって説明したことで有名です。
≪※3≫ 光子の進行速度( c )と波長( λ )の関係
光の発生メカニズムから説明されますように、光子のエネルギー E は、光子の振動数 ν のみによって決まります。(本連載第2回の註釈≪※2≫、≪※3≫を参照下さい。)
E = h ・ ν ( h :プランク定数 h = 6.6 × 10 -34[ J・s(ジュール・秒)])
光子が、その進行過程において、媒質(の構成分子・原子)との間でエネルギーのやり取りをするような特殊な場合を除き、一般的には媒質の種類・特性に関係なく、その光子の持つエネルギーは変化しません( E は一定)ので、異なる媒質の境界を横切ってもその前後で振動数 ν は変化しません。
光の進行速度c は、真空中で最大値 c = c0 ≒ 2.98 × 108 [ m / 秒 ](一定)となりますが、一般媒質中では
c = ν ・ λ = ( E / h )・ λ < c0
となり、真空中より遅くなり波長に比例する(波長が短いほど進行速度が遅くなる)ことになります。
デモ隊の例で言えば、舗装道路でも砂浜での歩調(振動数 ν )は一定で変わらないのですが、砂浜に進入したとたんに歩幅(波長 λ )が短くなり進行速度が遅くなることに対応します。
光と色の話 第一部

第23回 光の屈折
・・・・・ 光はなぜ媒質界面で屈折するのか? ・・・・・
はじめに
本連載の第 19 回では、虹の色についてお話しました。大気中に浮遊した水滴群で太陽の光が屈折するとき、光の波長によって屈折する角度が異なることが七色の虹の発生原因でした。光学分野では光の波長に依存して屈折する角度が変わることを「分散」と呼んでいます≪※1≫。
光の屈折現象については、小中学校時代に理科の授業で勉強しました。ガラスや水の面に光が斜めに入射すると、その界面で光の進行方向が変わる現象として学習した記憶がありますね。この屈折現象の結果、右下の写真のように、水を入れた器に差し込んだ棒が、水面のところで屈曲したように見えます。
このような物理現象が起こるということ自体は小中学校で勉強するのですが、透明物質の境界で光の進行方向が何故曲がるのか?については、おそらく大学などでの専門教育で勉強することになる、というのが一般的ではないかと思います。筆者の心が屈折しているのはなかなかうまく説明できませんが、光が屈折することは論理的に比較的説明しやすいと思います。光の屈折現象については、厳密には光の波動理論によって説明されるのですが、その前に、先ず(厳密さはさておいて)直感的な理解を助けるために、デモ行進を例え話にしてお話してみましょう。

屈折現象の直感的理解・・・・・デモ行進での例え話
隊列を組んで足並みを揃えて舗装道路上を直進するデモ隊を考えます。(最近はこのようなデモ隊は流行らなくなりましたが、昔は安保闘争などでよく見かけたものです。)足並みが揃っているということは、デモ隊の構成員全員の歩幅が等しくかつ歩調(例えば、1 分間に何歩踏み出すか)が揃っているということです。
その結果、デモ隊は [歩幅] × [歩調] の行進速度で整然と直進することになります。
これを光の進行に対応付けると、歩幅が光の波長( λ [ m ] )に、歩調が振動数( ν [ 1 / 秒 ] )に対応すると考えることができ、光の進行速度( c )は
c = ν ・ λ [ m / 秒 ] となります。
このデモ隊が舗装道路から砂浜へ進入していく場合を考えます。舗装道路から砂浜へ垂直に進入する場合は、デモ隊の横一列の構成員は一斉同時に砂浜へ足を踏み入れることになります。それまでは歩き易い舗装道路上を行進してきたのですが、砂浜では歩きにくいため、歩調は一定に保っても歩幅( λ )が短くなってしまい
( λ → λ’ < λ )、その結果、砂浜に入った直後から行進速度は落ちてしまいます
( c’ = ν ・ λ’ < c )。この現象が、砂浜に足を踏み入れる横一列毎に次々に起こることになり、砂浜でのデモ隊の行進速度は、舗装道路上よりも遅くなってしまいます。しかし、横一列が一斉同時に行進速度を落とすため、デモ隊の進行「方向」自体は変わらずそのまま直進することになります。

デモ隊が砂浜へ斜め方向から進入した場合はどうなるでしょうか?右図のような場合、デモ隊の進行方向に向かって左端に位置する人が最初に砂浜に足を踏み入れることになります。この人はその時点から行進速度が落ちてしまいますが、その一方、右端の人はまだ舗装道路上ですので、それまでの速い速度のまま行進を続けています。つまり、デモ隊の横一列の構成員の行進速度が落ちるタイミングにズレが発生することになります。その結果、デモ隊の進行方向は、必然的に、舗装道路と砂浜の境界線から遠ざかる方向へ変化することになります。

デモ隊が逆の向きに(砂浜から舗装道路へ)行進する場合は、上記とは逆に、舗装道路に足を踏み入れた時点から行進速度が速くなるため、隊列の進行方向は境界線に近づく方向に変化することになります。

以上が大雑把な屈折現象の直感的イメージです。光の屈折においては、舗装道路が例えば空気に対応し、砂浜が水やガラスに対応し、「歩きにくさ」が屈折率に相当します。実際、光の速度は空気中に比べて水やガラスの中では遅くなります。つまり、屈折現象とは、媒質によって光の速度が異なることが原因となって、異なる媒質の境界面で光の進行方向が変化する現象のことであると言えます。
光の波長によって屈折角が変わる現象(光の分散)の直感的理解
光の波長が短いほど屈折率が大きくなることは、以下のように考えれば直感的に解り易いように思います。
均一媒質中での光の速度 c は、振動数 ν と波長 λ の積で表わすことができ( c = ν ・ λ )、これはデモ隊の例では、
「行進速度 = 歩調 × 歩幅」に対応することは上述しました。
砂浜では、歩調が速いほど、砂浜に足先を踏み入れる機会が多くなりますので、より歩きにくくなり、行進速度は遅くなってしまいます。これは歩調が速いほど歩幅が狭くなってしまうことに対応します。つまり、振動数 ν が大きい(波長 λ が短い)ほど、光の速度が低下してしまいます。
その結果、例えば空気(舗装道路)から水(砂浜)に進行すると、波長 λ が短いほど水面(道路と砂浜の境界)から遠ざかる方向(屈折角が小さい方向)に大きく屈折することになります。

ホイヘンス( Huygens )≪※2≫ の原理
上記の光の屈折の説明は、多少正確さは犠牲にして、例え話により直感的な解り易さを優先したものです。光の屈折や反射の現象は、理論的には波動理論に基づくホイヘンスの原理によって説明されます。
ホイヘンスの原理とは、光を振動する波として捉え、その波が伝わる媒質の各点が新たな波源として周囲の各点に振動を伝え、次々と振動が伝播していくというもので、これらの各波の波面の包絡面が実際の波として観察される、というものです。
例えば平面波の場合、横一列に並んだ媒質の各点( P1 、P2 、・・・・)は同期して同一周波数で規則的に上下振動を繰り返しています。この内の1点に着目すると、この点の振動は同心円状(三次元の場合には同心球状)に周囲に波紋として広がって行くと考えられます。これを「素元波」と言います。この素元波が各点・について同時に発生すると考えられますので、結局、各素元波の共通接線す三次元の場合は共通接面すなわち包絡面)が実際の新しい波(波面)として観察されるという訳です。この波面上の各点がまた同様に新たな振動源となって、また新たな素元波を作り出し、新たな波面が生まれるということを繰り返して、波面に垂直な方向に平面波が伝播進行していくということになります。

空間の1点の振動が周囲に広がっていく場合(球面波)は、その点の周囲に発生した円形(三次元の場合には球形)の二次波(素元波)上の各点がまた新たな振動源となりそれぞれの点の周囲にまた素元波を発生させていきます。その結果、対応する素元波群の包絡線(三次元的には包絡面)も円形(球形)となり球面波が形成されます。波の進行方向は、波面に垂直な方向、すなわち、最初の震源点を中心として四方八方の全方向に均等に広がって行きます。

ホイヘンス( Huygens )の原理による屈折の説明
今、光が空気中からガラスの表面に斜めに入射する場合を考えます。この平面波を A 、B 、C 、D の 4 つの光線成分に分けて考えましょう。光は空気中では平面波として直進しています。つまり、それぞれの「素元波」 a 、b 、c 、d は同時並行的に広がって行き、それらの包絡面で構成される波面は光の進行方向に垂直な平面となります。図においては、波面を茶色(実線が「山」、破線が「谷」)で示しており、位相が揃った形で進行、入射して行く様子を模式的に描いています。
光は界面に対して斜めに入射していますので、まず光線成分 A が最初に界面 A1 に到達します。この時点で他の光線成分は、B1 、 C1 、D1 の位置まで進んでいます。界面に到達した光線成分 A はガラス(屈折率 > 1 )の内部に進行しますが、内部では進行速度が遅くなってしまいます。従って、光線成分 D が D1 から D2(界面)に到達した時点で、光線成分 A の「素元波」は a1 で示した位置まで伝播しています。同様に、光線成分 B 、C についてもそれぞれの「素元波」は b1 、c1 のような位置まで伝播しています。これらの素元波の包絡面として A2 B2 C2 D2 で示される平面が全体としての波面を構成することになり、光の進行方向はこの平面に垂直な方向となる、すなわち界面で屈折するということになる訳です。

屈折率が 1 より大きい媒質(水やガラスなど)の中では、光の進行速度は波長に依存し、波長が短い程進行速度が遅くなります≪※3≫。
従って、上記の説明において、波長が短い程、素元波 a1 、b1 、c1 の伝播速度が遅くなりますので、より大きく屈折することになります。
注釈
≪※1≫ 分散
「分散」という用語は、バラバラになることやそのバラツキの状態を表わす言葉として一般会話でもよく用いられますが、技術用語としては技術分野によって異なる定義で使用されています。
光学分野では、本文のように、光の波長(あるいは振動数)に依存して屈折角が変化することを「分散 dispersion 」と定義していますが、確率統計学分野では、確率事象のバラツキの程度を示す量である標準偏差の二乗を「分散 variance 」と言っています。(英語では、別の用語になっています。)
一般に、ひとつの用語に複数の定義があるのは、混乱の元となって好ましいことではないのですが、(光学分野と確率統計学分野のように)その用語が使用される分野が大きく離れている場合には、混乱を引き起こすことは少ないと考えられますので、事実上許容されているものと考えられます。
技術用語をどの定義の下で使用しているのかが明々白々である場合はともかく、そうでない場合は定義を明確にした上で使用すべきです。
≪※2≫ ホイヘンス Christiaan Huygens( 1629 - 1695 )
オランダの数学者、物理学者、天文学者。光学分野ではニュートンの光の粒子説に対して、ホイヘンスは光の波動説を唱え、光の反射・屈折現象を波動原理によって説明したことで有名です。
≪※3≫ 光子の進行速度( c )と波長( λ )の関係
光の発生メカニズムから説明されますように、光子のエネルギー E は、光子の振動数 ν のみによって決まります。(本連載第2回の註釈≪※2≫、≪※3≫を参照下さい。)
E = h ・ ν ( h :プランク定数 h = 6.6 × 10 -34[ J・s(ジュール・秒)])
光子が、その進行過程において、媒質(の構成分子・原子)との間でエネルギーのやり取りをするような特殊な場合を除き、一般的には媒質の種類・特性に関係なく、その光子の持つエネルギーは変化しません( E は一定)ので、異なる媒質の境界を横切ってもその前後で振動数 ν は変化しません。
光の進行速度c は、真空中で最大値 c = c0 ≒ 2.98 × 108 [ m / 秒 ](一定)となりますが、一般媒質中では
c = ν ・ λ = ( E / h )・ λ < c0
となり、真空中より遅くなり波長に比例する(波長が短いほど進行速度が遅くなる)ことになります。
デモ隊の例で言えば、舗装道路でも砂浜での歩調(振動数 ν )は一定で変わらないのですが、砂浜に進入したとたんに歩幅(波長 λ )が短くなり進行速度が遅くなることに対応します。

